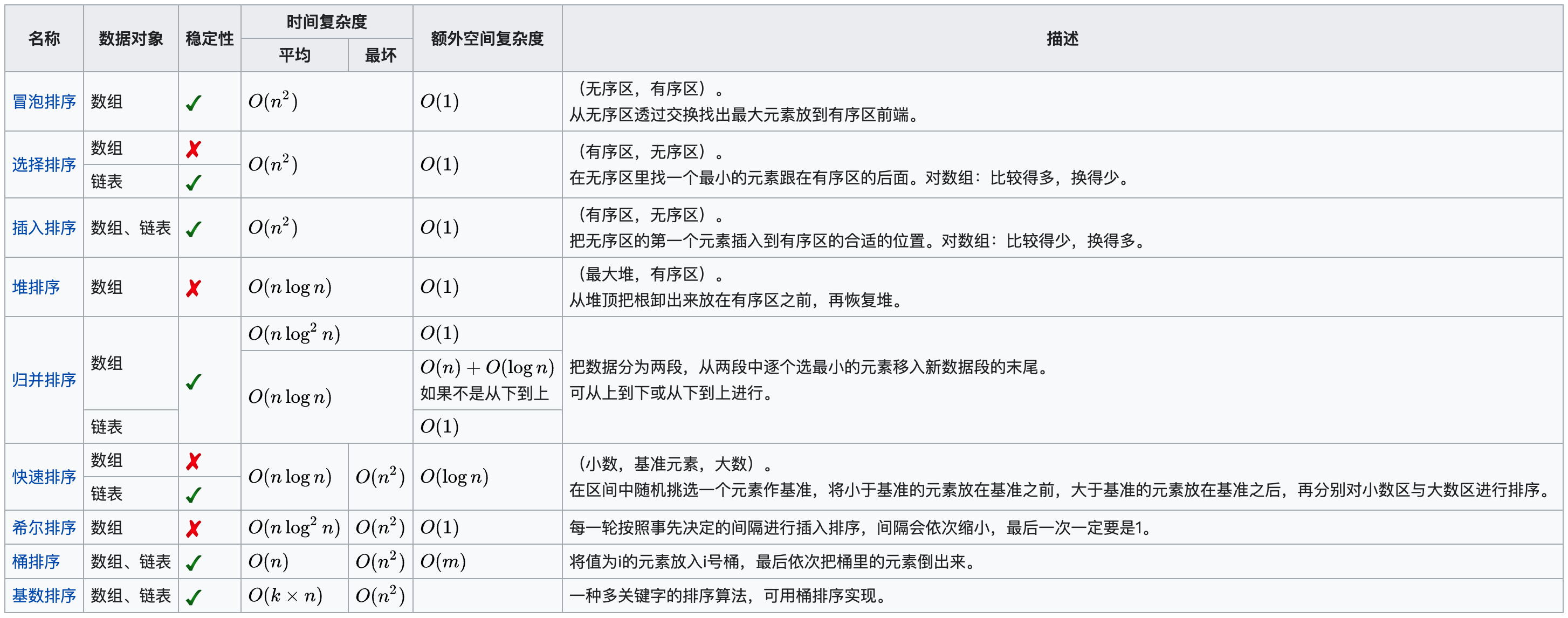
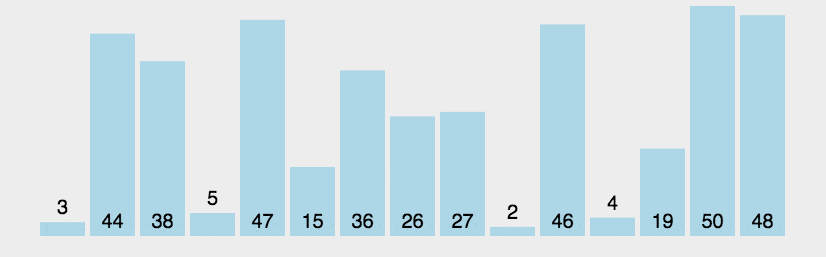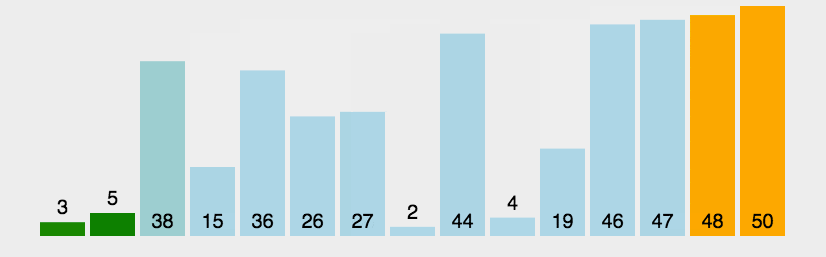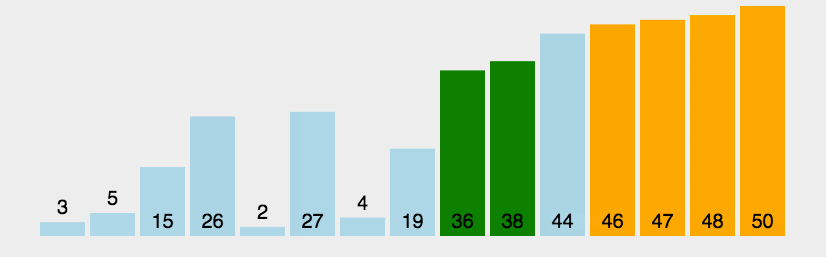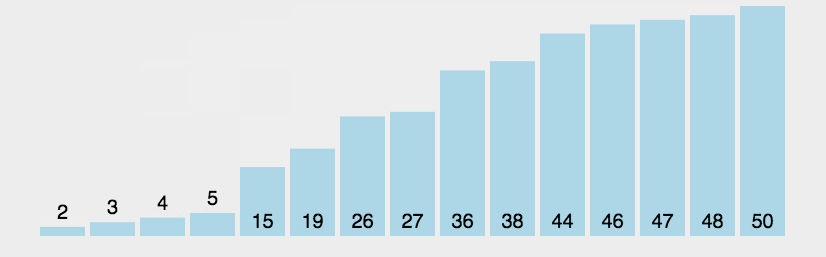排序算法,本文整理了之前个人学习中的九种常用的排序算法,用作个人引导复习使用,包括的方法如下图所示:
1. 冒泡排序(Bubble Sort)
原理: 比较相邻的元素。如果第一个比第二个大,就交换他们两个。对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,做完后,最后的元素会是最大的数。所有的元素重复以上的步骤,直到没有任何一对数字需要比较。
动图:
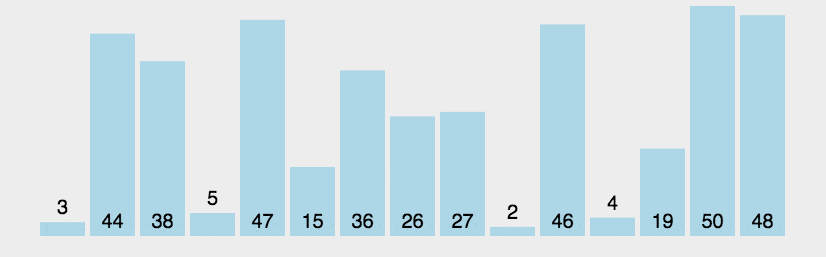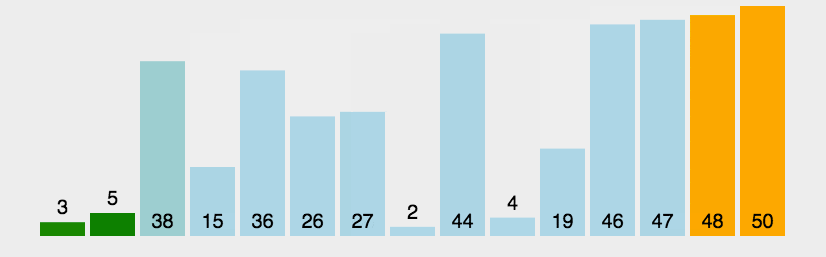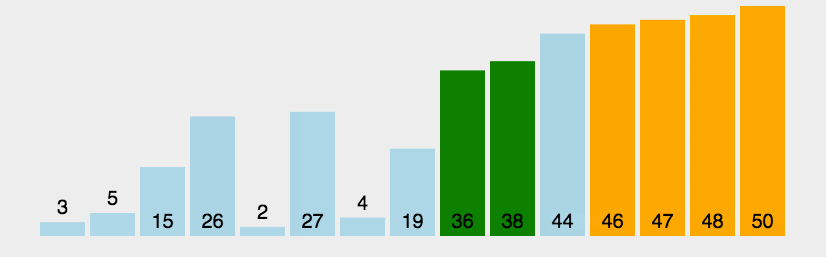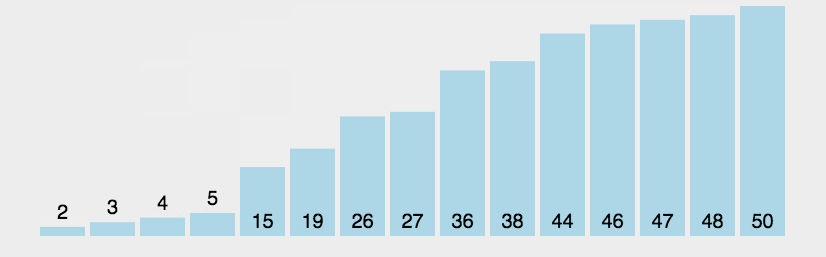
function bubbleSort(arr) {
for (let i = 0; i < arr.length - 1; i++) {
for (let j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j + 1], arr[j]] = [arr[j], arr[j + 1]];
}
}
}
return arr;
}
|
2. 选择排序(Selection Sort)
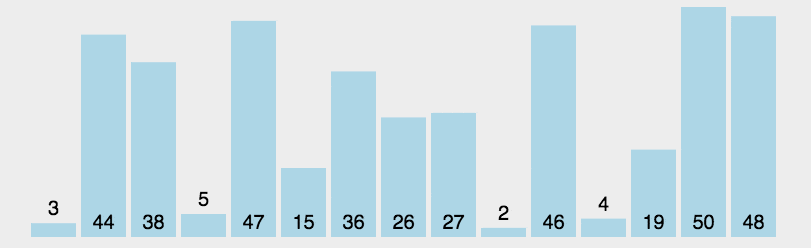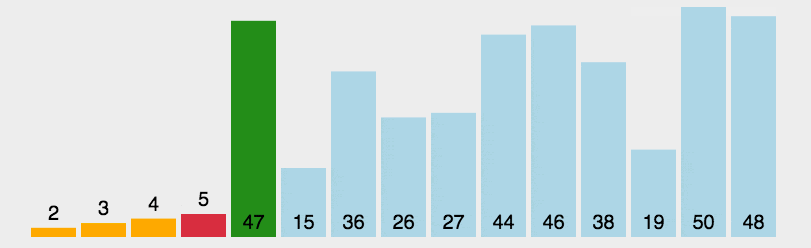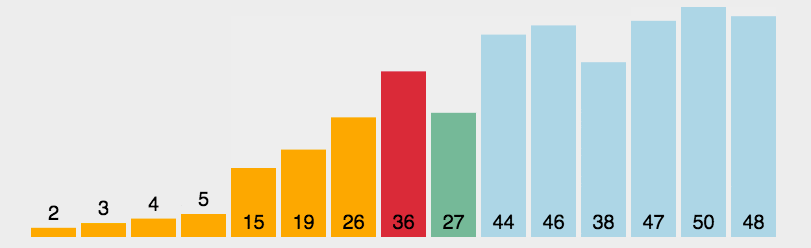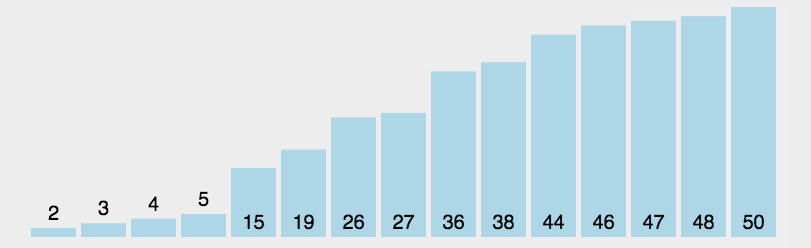
原理: 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。重复第二步,直到所有元素均排序完毕。
动图:
function selectionSort(arr) {
for (let i = 0; i < arr.length - 1; i++) {
let maxIndex = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] > arr[maxIndex]) {
maxIndex = j;
}
}
[arr[i], arr[maxIndex]] = [arr[maxIndex], arr[i]];
}
return arr;
}
|
3. 直接插入排序(Insertion Sort)
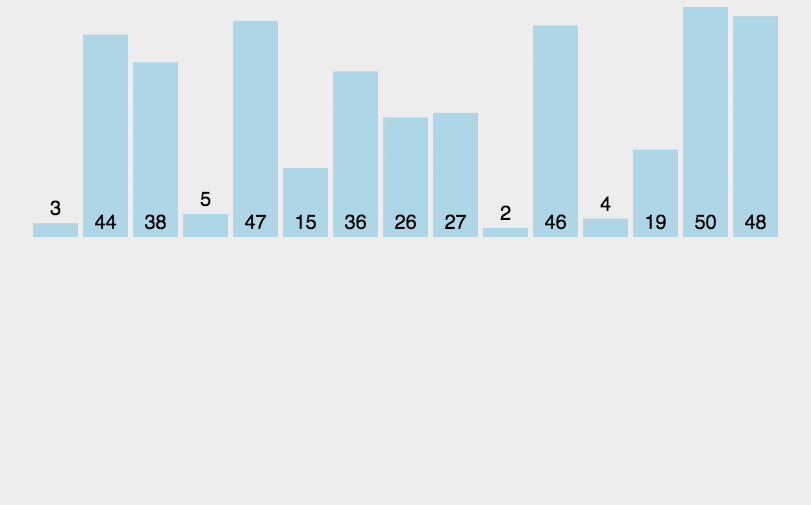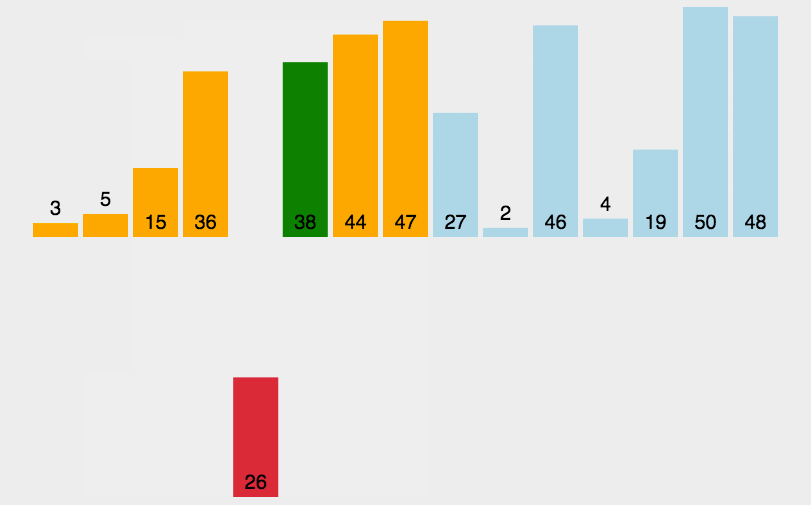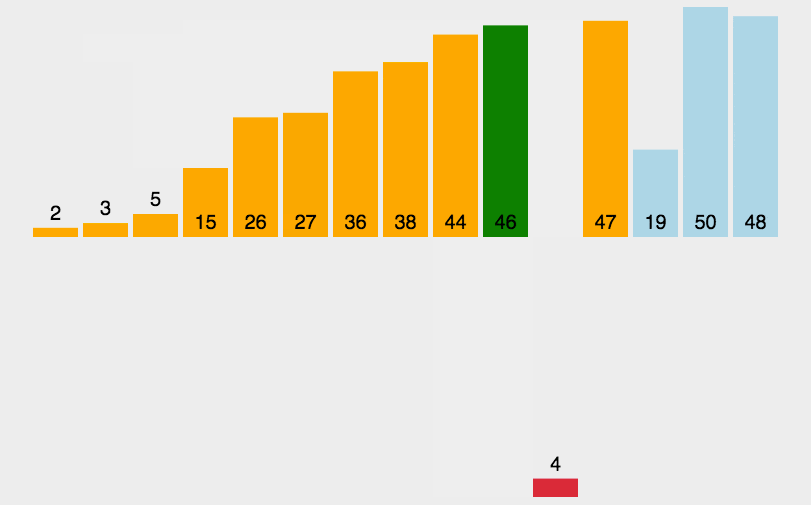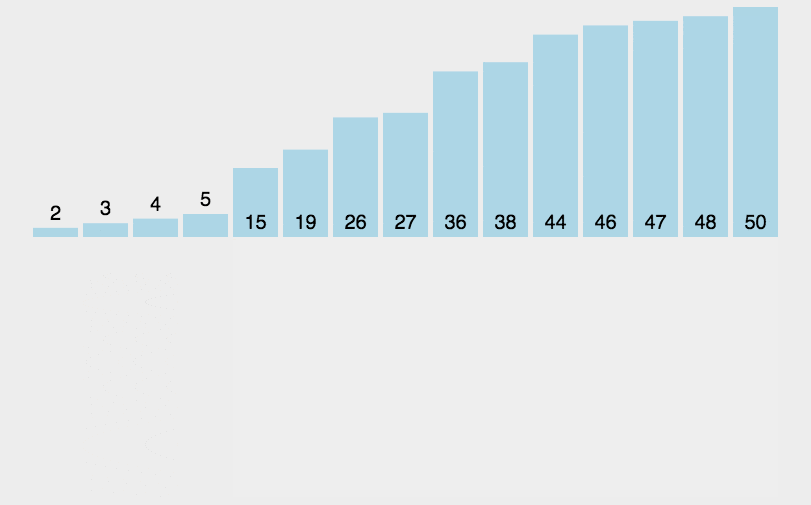
原理: 插入排序是一种最简单直观的排序算法,将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
动图:
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let preIndex = i - 1, currentNum = arr[i];
while (preIndex >= 0 && arr[preIndex] < currentNum) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = currentNum;
}
return arr;
}
|
4. 希尔排序(Shell Sort)
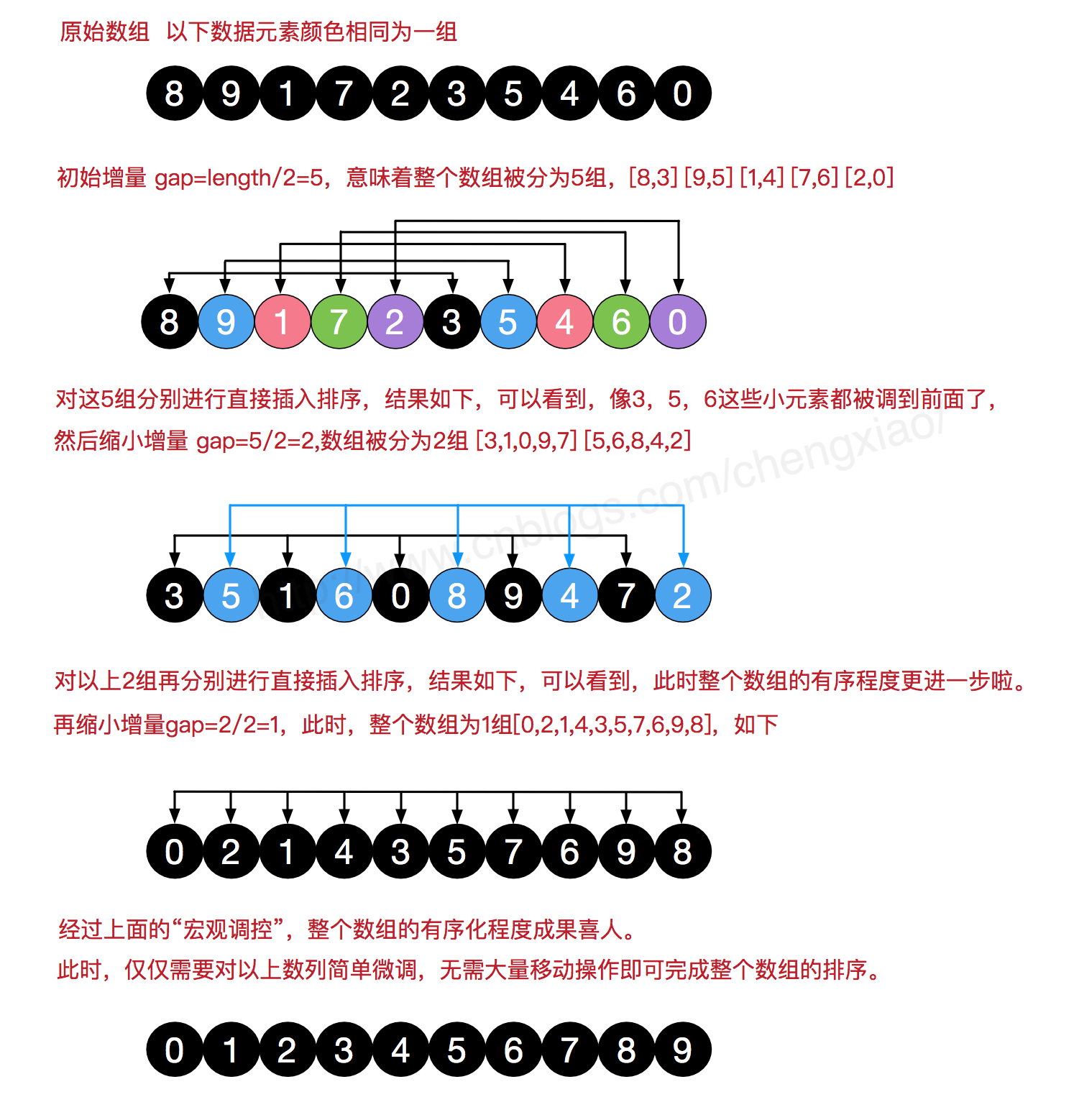
原理: 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
步骤:
直接插入排序的逆序的话首末端排序效率很低,希尔排序跳跃式分组,通过增量将元素分组,这样的话移动次数大大降低,然后缩小增量,直到增量为1;基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2…1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
function shellSort(arr) {
for (let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap / 2)) {
for (let i = gap; i < arr.length; i++) {
let j = i - gap;
let currentNum = arr[j + gap];
while (j >= 0 && arr[j] < currentNum) {
arr[j + gap] = arr[j];
j -= gap;
}
arr[j + gap] = currentNum;
}
}
return arr;
}
|
5. 快速排序(Quick Sort)
原理: 快速排序使用分治法,快排在平均状况下时间复杂度为Ο(nlogn),极限情况下是n的平方,但是这种状况极少而且快排明显比其他Ο(nlogn)的算法更快;
步骤:
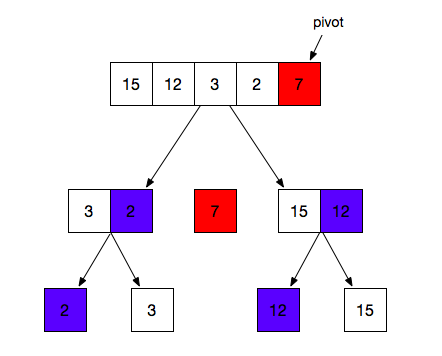
1 从数列中挑出一个元素,称为 “基准”(pivot);
2 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
3 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
let quickSort = function (arr) {
if (arr.length <= 1) {
return arr;
}
let pivot = arr.splice(Math.floor(arr.length / 2), 1)[0];
let left = [];
let right = [];
for (let i = 0; i < arr.length; i++) {
if (arr[i] > pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat(pivot, quickSort(right));
};
|
优缺点:
缺点:获取基准点使用了一个splice操作,在js中splice会对数组进行一次拷贝的操作,而它最坏的情况下复杂度为O(n),而O(n)代表着针对数组规模的大小进行了一次循环操作。我们每次执行都会使用到两个数组空间,增大空间复杂度;concat操作会对数组进行一次拷贝,而它的复杂度也会是O(n),对大量数据的排序来说相对会比较慢
优点:代码简单明了,可读性强,易于理解
6. 归并排序(Merge Sort)
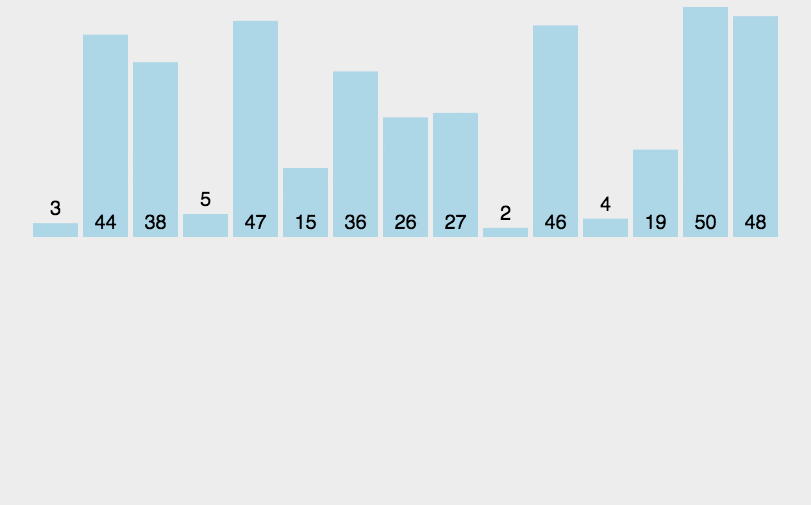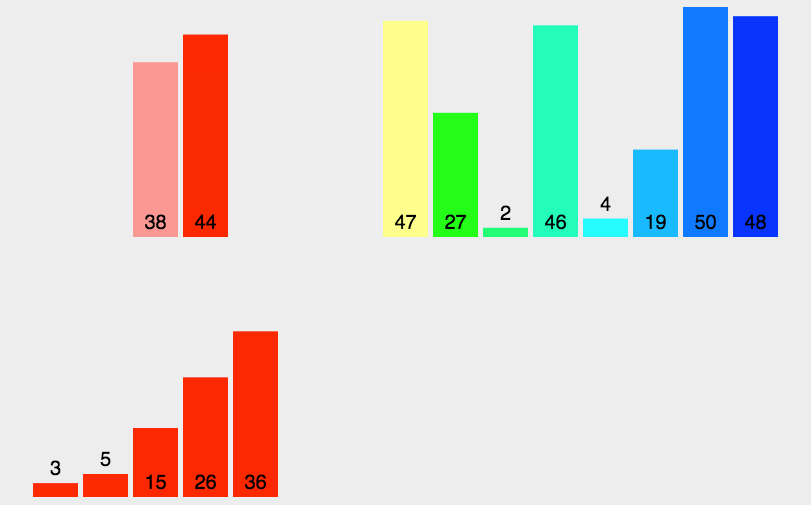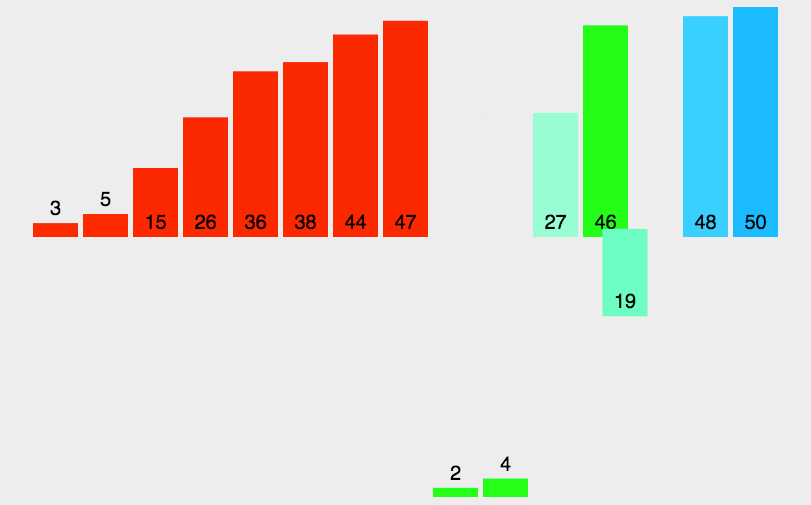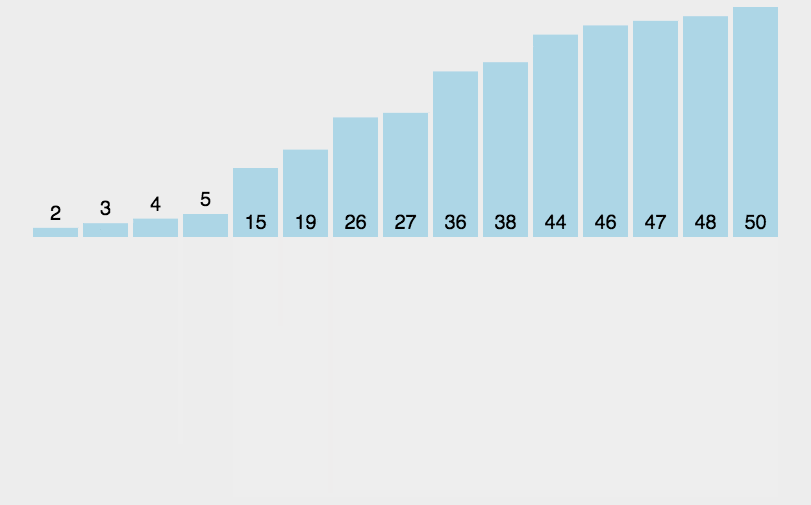
原理: 归并排序:将两个或者两个以上的有序表组合成一个新的有序表;待排表有n个元素,视为n个有序的子表,每个子表长度为1,两个归并后,得到n/2取上界个的长度为2或者1的有序表,然后继续合并,重复到一个长度为n的有序表终止。选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间
步骤:
如代码所示
function mergeSort(data) {
let len = data.length;
if (len < 2) {
return data;
}
let middle = Math.floor(len / 2),
left = data.slice(0, middle),
right = data.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
let merge = (left, right) => {
let result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
return result;
};
|
8. 基数排序(Radix Sort)
原理: 基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
步骤:
如代码所示,先将待排序数据放入到根据数据生成的对应的counter数组内的桶(数组)里,然后开始对个位进行排序,然后放入arr中,个位排序结束后,重新根据十位生成counter的桶,再对十位进行排序然后再放入arr中,直到最大位数也排序完成。

function radixSort(arr, maxDigits) {
let counter = [];
let mod = 10, dev = 1;
for (let i = 0; i < maxDigits; i++, dev *= 10, mod *= 10) {
for (let j = 0; j < arr.length; j++) {
let bucket = parseInt((arr[j] % mod) / dev);
if (counter[bucket] == null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
let pos = 0;
for (let j = counter.length - 1; j >= 0; j--) {
if (counter[j]) {
while (counter[j][0]) {
arr[pos++] = counter[j].shift();
}
}
}
}
return arr;
}
|
PS:本文参考地址这里,此链接。